A crucial goal of machine learning is to make inferences about a process based on the data collected from the same process. When deriving the error function of linear regression in a lecture, this process is assumed to be the distribution N (w⊤x, σ2), and the data is assumed to be drawn from this
process in an i.i.d. fashion. Since the inference is made using probabilistic arguments, we call this a probabilistic inference. In this problem, we shall estimate the average time E[T] until a student uploads a new post on Piazza.

• Let us model T ∼ Exp(λ) with an exponential distribution where λ = 1/E[T] is the reciprocal of the average time until a student uploads a new post on Piazza. Recall that the density function of T is p(t) = λ exp(−λt). Our goal is to find a best guess for λ, which we will denote as λˆ. We observed that the time intervals between the first 6 posts are D = {1.0, 2.0, 2.5, 1.0, 3.5} (note that |D| = 5). What is the log-likelihood ln p(D|λ) of observing D given λ?
  
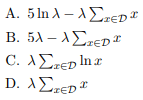
• What is the maximizer λˆ of the log-likelihood?
  
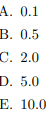
• Let us now introduce a prior distribution over the possible value of λ and find the posterior over the parameters p(λ|D). Which of the following are valid priors for λ? Check all that apply.
  A. Exponential distribution Exp(0.5) with rate parameter 0.5
  B. Uniform distribution U(0.5, 1.5) from 0.5 to 1.5
  C. Uniform distribution U(−1.0, 1.0) from −1.0 to 1.0
  D. Normal distribution N (0.0, 1.0) with mean 0.0 and variance 1.0